иЎҢжөӢж•°йҮҸе…ізі»и®Іе ӮвҖ”вҖ”зүӣеҗғиҚүй—®йўҳв‘
жқҘжәҗпјҡе®үеҫҪиҖғеҫ·дёҠе…¬еҹ№ж—¶й—ҙпјҡ2015-01-15
еӨ§з§‘еӯҰ家зүӣйЎҝжӣҫзј–иҝҮдёҖдёӘжңүи¶Јзҡ„й—®йўҳпјҡ
дҫӢ1гҖҒзү§еңәдёҠжңүдёҖзүҮйқ’иҚүпјҢжҜҸеӨ©зү§иҚүйғҪеҢҖйҖҹз”ҹй•ҝгҖӮиҝҷзүҮзү§иҚүеҸҜдҫӣ10еӨҙзүӣеҗғ22еӨ©пјӣжҲ–иҖ…еҸҜдҫӣ16еӨҙзүӣеҗғ10еӨ©пјӣеҰӮжһң25еӨҙзүӣеҗғиҝҷзүҮзү§иҚүпјҢиғҪеҗғеӨҡе°‘еӨ©пјҹ
иҝҷзұ»й—®йўҳеҸҲеӣ жӯӨиў«з§°дёәзүӣйЎҝй—®йўҳпјҢд»ҠеӨ©е®үеҫҪиҖғеҫ·дёҠ专家иҰҒеёҰе°Ҹдјҷдјҙ们еҘҪеҘҪиҝҺжҲҳеӨ§еёҲзҡ„й—®йўҳгҖӮ
зүӣеҗғиҚүй—®йўҳпјҢзңӢиө·жқҘи®©дәәж‘ёдёҚзқҖеӨҙи„‘пјҢдёҚзҹҘеҰӮдҪ•дёӢжүӢгҖӮе…¶е®һйҖҡиҝҮе·§еҰҷзҡ„жҖқз»ҙж–№ејҸиҪ¬еҸҳпјҢзүӣеҗғиҚүй—®йўҳеҸҜд»ҘиҪ¬еҢ–жҲҗ常规зҡ„е·ҘзЁӢй—®йўҳжқҘи§Јзӯ”пјҢеҰӮдҪ•иҪ¬еҢ–иҜ·з»ҶзңӢдёӢж–ҮгҖӮеҗ„дҪҚиҖғз”ҹе…¶е®һеҸӘиҰҒи®°дҪҸдёҖдёӘе…¬ејҸе°ұиғҪеҫҲиҪ»жқҫеҝ«йҖҹең°еә”еҜ№жүҖжңүзҡ„зүӣеҗғиҚүй—®йўҳгҖӮ
иҜ·еҠЎеҝ…зҶҹи®°иҝҷдёӘиҝһзӯүејҸпјҡM=пјҲN1пјҚxпјүt1=пјҲN2пјҚxпјүt2=пјҲN3пјҚxпјүt3=xT
е…¶дёӯпјҢMдёәеҺҹжңүиҚүйҮҸпјҢxдёәиҚүз”ҹй•ҝйҖҹеәҰпјҢN1гҖҒN2гҖҒN3дёәзүӣеӨҙж•°пјҢt1гҖҒt2гҖҒt3дёәзӣёеә”зҡ„ж—¶й—ҙпјӣTдёәиҚүеңәзҡ„жҒўеӨҚж—¶й—ҙгҖӮ
д»ҘдёӢзәўиүІж–Үеӯ—жҳҜдё“дҫӣеӯҰйңёзңӢзҡ„пјҢйҳҗиҝ°иҝҷдёӘе…¬ејҸжҳҜжҖҺд№ҲжқҘзҡ„пјҢеҜ№дәҺеҸӘдёәеә”д»ҳе…¬иҖғиҺ·еҫ—еҲҶж•°зҡ„еҗҢеӯҰеҸҜд»ҘзӣҙжҺҘи·іиҝҮгҖӮ
зҺ°еңЁе®үеҫҪиҖғеҫ·дёҠ专家з»ҷеӨ§е®¶и®Іи§ЈдёҖдёӢиҝҷдёӘиҝһзӯүејҸпјҢзҗҶи§ЈдәҶд№ӢеҗҺе°ұйқһеёёе®№жҳ“и®°дәҶгҖӮ
дёәдәҶз®ҖеҢ–й—®йўҳпјҢжҲ‘们еҒҮи®ҫжҜҸеӨҙзүӣжҜҸеӨ©еҗғ1д»ҪиҚүпјҢиҚүеңәжҜҸеӨ©з”ҹй•ҝxд»ҪиҚүпјҲиҝҷз§Қи®ҫжі•з”Ёзҡ„жҳҜзү№еҖјзҡ„жҖқжғіпјҢеӣ дёәзүӣеҗғиҚүйҖҹеәҰе’ҢиҚүз”ҹй•ҝйҖҹеәҰеҝ…然жҳҜдёҖдёӘжҜ”еҖјпјҢдёәдәҶз®ҖеҢ–и®Ўз®—жҲ‘们еҲҶеҲ«и®ҫдёә1е’ҢxпјӣеҒҮдҪҝжҲ‘们еҲҶеҲ«и®ҫдёәvе’ҢvxпјҢеҲҷеңЁи®Ўз®—иҝҮзЁӢдёӯvиў«зәҰеҲҶпјҢз»“жһңд»Қ然дёҖж ·пјүпјӣеӣ жӯӨжңүN1еӨҙзүӣж—¶пјҢжҜҸеӨ©е…ұеҗғжҺүN1д»ҪиҚүпјҢеҗҢж—¶иҚүеңәжҜҸеӨ©з”ҹй•ҝxд»ҪиҚүпјҢиҝҷж ·жҜҸеӨ©иҚүеңәеҮҖеҮҸе°‘N1-xд»ҪпјҢt1еӨ©еҗғе®Ңзҡ„еҗ«д№үе°ұжҳҜд»ҘжҜҸеӨ©еҮҖеҮҸе°‘N1-xд»ҪиҚүзҡ„йҖҹеәҰи®©еҺҹжңүзҡ„Mд»ҪиҚүеҮҸе°‘дёә0пјӣдәҺжҳҜеҸҜд»Ҙеҫ—еҮәM=пјҲN1пјҚxпјүt1пјӣеҗҢж ·зҡ„йҒ“зҗҶпјҢжҲ‘们еҸҜд»Ҙеҫ—еҮәM=пјҲN2пјҚxпјүt2е’ҢM=пјҲN3пјҚxпјүt3гҖӮжҒўеӨҚж—¶й—ҙTзҡ„еҗ«д№үжҳҜиҝҷзүҮиҚүеңәд»Һж— еҲ°жңүпјҲиҚүйҮҸд»Һ0еҲ°Mд»ҪпјүжүҖйңҖиҰҒзҡ„ж—¶й—ҙпјҢеҚід»ҘжҜҸеӨ©з”ҹй•ҝxд»Ҫзү§иҚүзҡ„йҖҹеәҰи®©иҚүеңәд»ҺиҚүйҮҸдёә0з§ҜзҙҜеҲ°Mд»ҪжүҖйңҖзҡ„ж—¶й—ҙпјҢеӣ жӯӨM=xTгҖӮеӨ§е®¶иҰҒжіЁж„Ҹзҡ„жҳҜеҚідҪҝиҚүеңәиҚүйҮҸдёә0пјҢең°дёӢйғЁеҲҶиҝҳжңүпјҢжүҖд»Ҙе…¶з”ҹй•ҝйҖҹеәҰдҫқ然жҳҜxпјҲеҪ“然иҝҷжҳҜзҗҶжғіеҢ–зҡ„жЁЎеһӢпјҢеҢ…жӢ¬еүҚж–Үзҡ„еҒҮи®ҫпјҢйғҪеҫҲзҗҶжғіеҢ–гҖӮеӨ§е®¶дёҚиҰҒзә з»“пјҢеӣ дёәж•°еӯҰжң¬иә«е°ұжҳҜеҜ№зҺ°е®һз”ҹжҙ»зҡ„з®ҖеҢ–е’ҢзҗҶжғіеҢ–пјүгҖӮз»јеҗҲд№ӢеҗҺпјҢе°ұжҳҜд»ҘдёҠзҡ„иҝһзӯүејҸдәҶгҖӮ
гҖҗи§ЈжһҗгҖ‘пјҡеӣ жӯӨеҜ№дәҺж–ҮдёӯејҖе§Ӣзҡ„дҫӢ1пјҢеҸҜеҲ—ејҸеҰӮдёӢпјҡпјҲ10пјҚxпјүГ—22=пјҲ16пјҚxпјүГ—10=пјҲ25пјҚxпјүtпјӣеӣ дёәжӯӨеӨ„дёҚйңҖжұӮжҒўеӨҚж—¶й—ҙTпјҢжүҖд»ҘM=xTе°ұж— йңҖеҲ—еҮәжқҘпјӣеӨ§йғЁеҲҶзүӣеҗғиҚүй—®йўҳйғҪжҳҜиҝҷз§Қжғ…еҶөпјҢиҝҷж—¶з”»иӣҮе°ұж— йңҖж·»и¶ідәҶгҖӮ
йӮЈд№Ҳе…¬ејҸеҲ—еҮәжқҘдәҶпјҢеҰӮдҪ•еҝ«йҖҹең°жұӮи§Је‘ўпјҹе®үеҫҪиҖғеҫ·дёҠ专家жҸҗйҶ’еӨ§е®¶пјҡе…ій”®жҳҜжұӮеҮәиҚүз”ҹй•ҝйҖҹеәҰxпјҒиҜ·иҖғз”ҹеҠЎеҝ…еҶҚи®°дҪҸдёҖдёӘе…¬ејҸпјҡ
жүҖд»ҘеҲҡжүҚйӮЈдёҖйўҳпјҡ
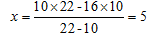 пјӣеҶҚе°Ҷxд»Је…ҘиҝһзӯүејҸпјҢи§ЈеҮәt=5.5еӨ©пјӣеӨҹ25еӨҙзүӣеҗғ5.5еӨ©
пјӣеҶҚе°Ҷxд»Је…ҘиҝһзӯүејҸпјҢи§ЈеҮәt=5.5еӨ©пјӣеӨҹ25еӨҙзүӣеҗғ5.5еӨ©
еҸӘиҰҒжҢүз…§иҝҷдёӘжҖқи·ҜпјҢиҝҷдёҖзұ»й—®йўҳеңЁеҚҠеҲҶй’ҹеҶ…е°ұиғҪи§ЈеҮәпјҢиҖҢдё”еӣ дёәи®Ўз®—йҮҸе°ҸпјҢеҮҶзЎ®зҺҮеҹәжң¬дёҠ100%пјҒ
еҶҚз»ғдёҖйўҳпјҡ
дҫӢ2гҖҒз§ӢеӨ©жқҘдәҶпјҢзү§еңәдёҠзҡ„иҚүдёҚд»…дёҚй•ҝеӨ§пјҢеҸҚиҖҢд»Ҙеӣәе®ҡзҡ„йҖҹеәҰеңЁеҮҸе°‘гҖӮе·ІзҹҘжҹҗеқ—иҚүең°дёҠзҡ„иҚүеҸҜдҫӣ20еӨҙзүӣеҗғ5еӨ©пјҢжҲ–еҸҜдҫӣ15еӨҙзүӣеҗғ6еӨ©гҖӮз…§жӯӨи®Ўз®—пјҢеҸҜдҫӣеӨҡе°‘еӨҙзүӣеҗғ10еӨ©пјҹ
гҖҗи§ЈжһҗгҖ‘пјҡиҝҷйҮҢзҡ„иҚүд»Ҙеӣәе®ҡзҡ„йҖҹеәҰеңЁеҮҸе°‘пјҢеӨ§е®¶е°ұжүӢи¶іж— жҺӘдәҶеҗ—пјҹжіЁж„ҸпјҢжҲ‘们еӯҰиҝҮиҙҹж•°пјҢзҹҘйҒ“вҖңиҙҹзҝҒвҖқзҡ„жҰӮеҝөпјҢйӮЈд№ҲиҝҳжғідёҚйҖҡеҮҸе°‘е°ұжҳҜиҙҹз”ҹй•ҝеҚіиҚүз”ҹй•ҝйҖҹеәҰxдёәиҙҹж•°еҗ—пјҹиҝҷд№ҹе°ұжҳҜеүҚж–ҮжүҖиҜҙиҚүз”ҹй•ҝйҖҹеәҰxеҸҜд»Ҙдёәиҙҹж•°зҡ„еҗ«д№үгҖӮ
еҲ—ејҸпјҡпјҲ20пјҚxпјүГ—5=пјҲ15пјҚxпјүГ—6=пјҲNпјҚxпјү10пјӣ
жұӮи§Јпјҡ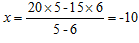 пјӣжңҖеҗҺд»Је…ҘжұӮеҫ—N=5пјӣеӣ жӯӨеӨҹ5еӨҙзүӣеҗғ10еӨ©гҖӮ
пјӣжңҖеҗҺд»Је…ҘжұӮеҫ—N=5пјӣеӣ жӯӨеӨҹ5еӨҙзүӣеҗғ10еӨ©гҖӮ
жӯӨйўҳдёӯиҚүз”ҹй•ҝйҖҹеәҰдёә-10пјҢд№ҹе°ұжҳҜиҚүжҜҸеӨ©еҮҸе°‘10д»ҪгҖӮ
дҫӢ3гҖҒзү§еңәдёҠй•ҝж»Ўзү§иҚүпјҢжҜҸеӨ©зү§иҚүйғҪеқҮеҢҖз”ҹй•ҝпјҢиҝҷзүҮзү§иҚүеҸҜдҫӣ10еӨҙзүӣеҗғ20еӨ©пјҢеҸҜдҫӣ15еӨҙзүӣеҗғ10еӨ©пјҢеҲҷзү§еңәдёҠжңҖеӨҡж”ҫеӨҡе°‘зүӣпјҢиҚүж°ёиҝңеҗғдёҚе®Ңпјҹ
гҖҗи§ЈжһҗгҖ‘пјҡжҲ‘们дёҖиө·жқҘз ”з©¶вҖңжңҖеӨҡж”ҫеӨҡе°‘зүӣпјҢиҚүж°ёиҝңеҗғдёҚе®ҢвҖқзҡ„й—®йўҳгҖӮеӨ§е®¶иҜ•жғідёҖдёӢпјҢиҚүеңәеҺҹжңүMд»ҪиҚүпјҢеҰӮжһңжңүNеӨҙзүӣеҗғпјҢеҲҷжҜҸеӨ©еҮҖеҮҸе°‘N-xд»ҪиҚүгҖӮеҪ“жҜҸеӨ©еҮҖеҮҸе°‘иҚүйҮҸдёәжӯЈж•°пјҢдёҚз®Ўе…¶еҖјеӨҡд№Ҳе°ҸпјҢеҒҮд»Ҙж—¶ж—ҘпјҢеҲҷдёҖе®ҡиғҪеӨҹж…ўж…ўеҗғе®ҢпјӣеҪ“жҜҸеӨ©еҮҖеҮҸе°‘иҚүйҮҸдёәиҙҹж•°пјҢеҚіжҜҸеӨ©иҚүеңәиҚүйҮҸдёҚеҮҸеҸҚеўһж—¶пјҢеҲҷиҚүйҮҸеҸӘдјҡи¶ҠжқҘи¶ҠеӨҡпјҢж°ёиҝңеҗғдёҚе®ҢпјӣеҪ“жҜҸеӨ©еҮҖеҮҸе°‘иҚүйҮҸдёә0пјҢеҚіжҜҸеӨ©иҚүеңәй•ҝеҮәжқҘзҡ„иҚүеҲҡеҘҪиў«зүӣеҗғе®ҢпјҢеҲҷиҚүйҮҸе§Ӣз»ҲдҝқжҢҒдёҚеҸҳпјҢеҗҢж ·ж°ёиҝңеҗғдёҚе®ҢпјҢе®һзҺ°дәҶеҸҜжҢҒз»ӯеҸ‘еұ•гҖӮеӣ жӯӨиҚүж°ёиҝңеҗғдёҚе®Ңе°ұиҰҒж»Ўи¶іпјҡNвүӨxпјӣеҚіиҰҒи®©иҚүж°ёиҝңеҗғдёҚе®ҢжңҖеӨҡеҸҜдҫӣе…»Nmax=xеӨҙзүӣгҖӮ
еҲ—ејҸпјҡпјҲ10пјҚxпјүГ—20=пјҲ15пјҚxпјүГ—10пјӣ
жұӮи§Јпјҡ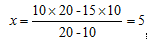 пјӣиҝҷзүҮзү§еңәзҡ„иҚүжңҖеӨҡеӨҹ5еӨҙзүӣж°ёиҝңеҗғдёҚе®ҢгҖӮ
пјӣиҝҷзүҮзү§еңәзҡ„иҚүжңҖеӨҡеӨҹ5еӨҙзүӣж°ёиҝңеҗғдёҚе®ҢгҖӮ
зүӣеҗғиҚүй—®йўҳжңҖеҺҹе§Ӣзҡ„йўҳеһӢе°ұжҳҜиҝҷж ·иҪ»жқҫиў«жҗһе®ҡзҡ„гҖӮ然иҖҢеңЁе…¬иҖғдёӯеҫҲеӨҡйўҳеҮәзҡ„йқһеёёйҡҗи”ҪпјҢиҷҪ然еұһдәҺзүӣеҗғиҚүзҡ„зұ»еһӢпјҢдҪҶеҚҙдёҚеҮәзҺ°вҖңзүӣвҖқе’ҢвҖңиҚүвҖқзҡ„еӯ—ж ·гҖӮйӮЈд№ҲеҜ№дәҺиҝҷдәӣй—®йўҳпјҢжҲ‘们еҰӮдҪ•еҒҡеҲ°ж…§зңјиҜҶйўҳе‘ўпјҢиҜ·еӨ§е®¶е…іжіЁе®үеҫҪиҖғеҫ·дёҠиЎҢжөӢеӨ©еӨ©з»ғжҜҸжңҹпјҢ继з»ӯе…іжіЁдёӢдёҖжңҹзҡ„вҖңиЎҢжөӢжҜҸе‘Ёи®Іе ӮвҖқгҖӮ